Happy Holidays, and Merry Christmas to all who celebrate it! While we at the Pressé Labs are hard at work on our next scientific endeavors, I’d like to take today to look at something a bit less serious: D&D!

What is Dungeons and Dragons?

For those who are unfamiliar, Dungeons & Dragons (D&D) is a collaborative tabletop role-playing game. One player, called the Dungeon Master (DM), establishes a world with people, towns, monsters and more, while the other players each create fantasy adventurers, called Player Characters (PCs), that explore and interact with their fellow PCs and the world the DMs creates. In interacting with the world, if a PC attempts to do something with a chance of failure, such as climbing the walls of a castle, haggling with a merchant, or attacking a goblin, the DM can call for a roll of a die to determine the outcome. The dice are labeled according to its number of faces (e.g. the normal cube die is called a d6). The official rule books give guidelines for what to roll and when, and how to interpret the results.

Here, I wish to analyze the melee combat capabilities of one of the martial player classes, the Fighter. Fighters benefit from being able to use the full variety of weapons and armor, and can select a Fighting Style to further specify their play-style. While many factors go into combat in D&D, here we are focusing on the expected damage per turn, so we will focus on offensive builds with powerful weapons and ignore defense.

What goes into an attack?

For a melee weapon attack, there are two sets of dice rolls used to determine the result. The attack rolls are used to determine whether an attack will hit or miss the defender, and the damage rolls are used to determine the damage done by the attack.

Attack Rolls

When making an attack roll, to start you roll a d20. Next, you add the appropriate ability modifier. This is a measure of your character’s raw ability to make the attack, whether due to physical prowess or nimble maneuverability, and is in an integer in the range of [-5, 5]. Next, if you are attacking with a weapon you are proficient with (which you generally are, especially if you play a martial character), you can add your character’s proficiency bonus. This number depends on your character level and goes from 2 to 6. Finally, you take your total and compare it to the enemy you are trying to hit’s armor class (AC). If you total is greater than or equal to your enemy’s AC, you hit an can roll for damage. If the total is less than the AC, it is considered a miss and you do no damage.

Furthermore, there are special effects for rolling a 1 or 20 on the d20. If you roll a 20, it is considered a critical hit. This means you automatically hit, and you roll twice as many dice as you would have on a regular hit. If you roll a 1, it is a critical miss and you miss regardless of any bonuses you have to the roll.

Damage Rolls

Once you hit with your attack, you get to roll damage. Each weapon has an associated number and type of dice. For example, a glaive deals 1d10 damage and a greatsword deals 2d6 damage. As mentioned previously, you roll twice as many dice as you otherwise would on a critical hit. Once you sum the rolls on your damage dice, you add the ability modifier you used in the attack roll, and the result is your total damage for that attack.

Of course, this is just the most basic algorithm for calculating the attack rolls and damage output. As your character increases in level, you character can gain abilities which increase their damage output. Let’s go over the ones that we will be considering for this exercise.

Fighting Style

Fighters and Paladins both choose a Fighting Style at early levels that allows them to specialize in combat. Two Fighting Styles are of interest to us for this exercise: Great Weapon Fighting and Two-Weapon Fighting.

Great Weapon Fighting

When your character is attacking with a weapon they hold in two hands, like a greataxe or a glaive, while rolling damage dice, if you have this fighting style you can reroll any dice that land on a 1 or a 2. Note that if the rerolls dice land on 1 or 2, you don’t get to reroll again.

Two Weapon Fighting

In D&D, when use you use an Action to attack with a weapon held in one hand, you can use a Bonus Action to make one extra attack with a weapon held in your other hand. Taking the Two Weapon Fighting Style removes the downside that the offhand attack does not add your ability modifier to damage rolls.

Feats

As your character progresses, you can choose from a number of unique features that give them extra abilities or bonuses. While some of the feats have abilities beyond what I mention here, I will only be considering the parts that directly affect our calculations.

Great Weapon Master

If your character has this feat, if you land a critical hit against an enemy, you may make an additional attack as a Bonus Action. Moreover, when making an attack roll you may choose to reduce your attack roll total by 5 for the benefit of increasing your damage roll total by 10.

Polearm Master

When using specific weapons, like a glaive or spear, you can use a bonus action to attack with the blunt end, with the damage dice being a d4.

Dual Wielder

This feat removes the restriction on what weapons can be wielded when two weapon fighting, allowing you to use any one-handed weapons.

Ability Score Increase

This allows you to raise your ability scores, effectively raising your ability score modifier by 1.

Advantage

Many situations will give you advantage on your attacks. When you attack with advantage, during the attack roll, you roll the d20 twice and use the higher roll.

Calculating Average Damage

Now that I have listed out the factors that I will be considering in my calculations, I create Julia code that will determine the average damage per turn based on character builds. Firstly, I create two functions that determine the average total damage for the dice rolled, one that handles regular die rolls, and one that deals with rolls that benefit from the great weapon fighting style. The regular average roll is straightforward, the average of the integers between 1 and the number of die faces:

function avgdicetot(num_dice, num_faces)
    avg_die_roll = (num_faces + 1) / 2
    avg_dice_total = num_dice * avg_die_roll
    return avg_dice_total
end

The great weapon average roll is a bit trickier, as we have to consider the case where we don’t roll a 1 or 2, the average between 3 and n, and then consider when we roll a 1 or 2, reducing back to the original case.

function avggreatdicetot(num_dice, num_faces)
    avg_die_roll = ((num_faces - 2) * (num_faces + 3) / 2 + num_faces + 1)/ num_faces
    avg_dice_total = num_dice * avg_die_roll
    return avg_dice_total
end

Next, I create a function that calculated the odds of hitting with an attack roll, but not landing a critical hit. I add in critical effects later simply because of the effect that critical hits have on the number of dice rolled. If the attack roll does not have advantage, then the odds of hitting (but not critting) are merely 20 minus the minimum die roll necessary to hit, divide by 20. If you have advantage, the odds become 1 minus the odds of rolling two missing numbers then subtracting the odds of a critical hit (39/400). One additional note on this step is that the bounds on these odds are the same regardless of whether or not you have advantage. The minimum odds are 0 and the maximum is 9/10.

function chancehitnocrit(AC, ability_mod, prof_bonus, gwm, adv)
    raw_calc = 20 + ability_mod + prof_bonus - AC
    if gwm
        raw_calc = raw_calc - 5
    end
    if adv
        odds = (400 - (19 - raw_calc) ^ 2 - 39) / 400
    else
        odds = raw_calc / 20
    end
    if raw_calc > 18
        return 9/10
    elseif raw_calc < 0
        return 0
    else
        return odds
    end
end

Finally, I implement the function that outputs the average damage as a function of AC. All of the factors we mentioned previously are implemented as boolean variables. We call the corresponding function to determine what the average dice roll will be given that we hit, then multiply it by the odds that we hit but don’t crit. Then, we factor in the odds of critical hits, and account for the fact that the damage dice is doubled on a crit, but the ability modifier is not affected. Finally, we add in the damage from any bonus attacks granted by our build.

function avgdamagespread(num_dice, ability_mod, prof_bonus, num_faces, gwf, gwm, gwm_dmg_up, pam, adv, num_hits)
    if gwf
        avg_dice_total = avggreatdicetot(num_dice, num_faces) 
    else
        avg_dice_total = avgdicetot(num_dice, num_faces)
    end
    avg_damage_array = zeros(length(AC_spread))

    for i in 1:length(AC_spread)
        no_crit = chancehitnocrit(AC_spread[i], ability_mod, prof_bonus, gwm_dmg_up, adv)
        avg_damage_array[i] = num_hits * ((no_crit + ifelse(adv, 0.195, 0.1)) * avg_dice_total 
            + (no_crit + ifelse(adv, 0.0975, 0.05)) * (ability_mod + ifelse(gwm_dmg_up, 10, 0)))
        if pam
            avg_bonus_total = ifelse(gwf, avggreatdicetot(1, 4), avgdicetot(1,4))
            avg_damage_array[i] = avg_damage_array[i] + ((no_crit + 
                ifelse(adv, 0.195, 0.1)) * avg_bonus_total + (no_crit + ifelse(adv, 0.0975, 0.05)) * ability_mod)
        elseif gwm
            avg_damage_array[i] = avg_damage_array[i] + (1 - (ifelse(adv, 361/400,19/20) ^ num_hits)) * ((no_crit + 
                ifelse(adv, 0.0975, 0.05)) * avg_dice_total + (no_crit + ifelse(adv, 0.195, 0.1)) * (ability_mod 
                + ifelse(gwm_dmg_up, 10, 0)))
        end
    end
    return avg_damage_array
end

Testing Builds

Now that our code is ready to handle the calculations, let’s consider 3 different situations and compare how each character build fares.

Level 1 Characters

Let’s suppose we have three level 1 characters, one with the Two Weapon Fighting Style and using two shortswords (1d6 damage), and two with the Great Weapon Fighting Style using a greataxe (1d12 damage) and a greatsword (2d6 damage). They otherwise have the same stats (Strength Modifier of +3, Proficiency Bonus of +2), and have not reached a level where they can select a feat.

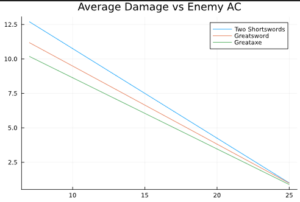
We see that the two shortswords outperform the greatsword and greataxe at all ACs. At this low level, the benefit of adding the Strength modifier twice instead of once outweighs the benefit of the Great Weapon Fighting Style. We also see that the greataxe is outclassed by the greatsword, which makes sense. The average die roll of 2d6 is going to be greater than that of 1d12.

Level 5 Characters

Now let’s consider a more complicated situation, characters at Level 5. The characters now have one more base attack and their proficiency bonus have increased to 3. Moreover, they get to choose one feat. We will be ignoring the builds that don’t synergize (like Great Weapon Master on a character using two short swords) and consider the potential builds. Furthermore, we replace our greataxe user with a glaive (1d10 damage) user to take advantage of the Polearm Master feat. Note that we assume the character with the Great Weapon Master feat will only use the -5/+10 to rolls when it is advantageous to do so.

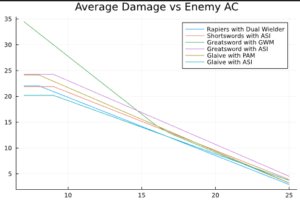
Here, we note some interesting behavior. Firstly, many of the builds feature a region where damage vs AC is flat. This is because at these low ACs, the only way for an attack to miss or for it to miss critically, so there is no AC dependence in the calculation of average damage. We notice at low ACs, the Greatsword with Great Weapon Master significantly outperforms the other options. When the odds of hitting an enemy are already high, the benefits are much easier to reap. However, when the odds to hit are lower, we instead see a standard ability score increase take the lead. The increased odds of landing a hit combined with the minor damage increase lead to the ASI being the best choice against stronger enemies.

Level 5 Characters with Advantage

Our final considered scenario involves the same characters as in the previous case, but now they are given advantage on their attacks.

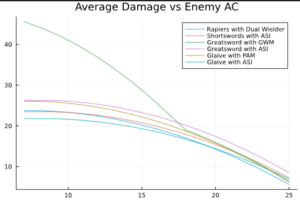
We see similar behavior as before, with two main differences. Firstly, the linear relationship between average damage and AC is gone. This is due to the odds of rolling specific numbers no longer being constant. The high numbers are more likely to occur due to low numbers, so the changes in average damage change less at low ACs, as it only affects unlikely outcomes. Secondly, we see the dominance of Great Weapon Master with a Greatsword lasts longer. This, again, is due to the odds of rolling high, and thus hitting an attack, are increased. Thus, it takes a higher AC for the ASI to catch up to the damage output.

Afterwords

Of course, this information should not be taken as the end all be all for character builds. Firstly, this analysis fails to account for character defenses, as well as positioning and maneuvering. Furthermore, many builds only become powerful at later levels. The Polearm Master and Great Weapon Master feat combined are often considered one of the most powerful builds in the game. This of course, requires you to have two feats, and you’ll want your Strength to be up to the task to make the most out of your attacks. What the best build is often depends on what tier of play your game is in, and many campaigns don’t make it too far beyond level 10. However, the tools presented here should provide a way to mathematically check the damage output of potential character builds.